A LUCKY GUESS - PART 2
You’ve arrived at your local testing center to take an ACT test. Anticipation hangs thick in the air across the students, but not you. As the test begins, you don’t even open the test booklet. You just start to bubble in questions randomly, moving your way across the page methodically. Then you put your head down and nap, waiting for the section’s end. For the next section, and the ones to follow, you do the exact same thing, guessing every single question without opening the test booklet.
Almost certainly, you’ve failed the test spectacularly. Your predicted score would be around a 12 out of 36, depending on the test. But imagine, just for a moment, that you somehow aced the test with a perfect 36. How likely is a perfect 36 earned entirely by blind luck?
To break this down, let’s start with the anatomy of the ACT test. The first section contains 75 questions with four options each. The next section has 60 questions with five options each. The third and fourth sections each have 40 questions with four options. This totals to 155 questions with four options each and 60 questions with five options.
This makes the cumulative probability of blindly acing the test
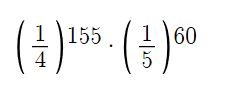
which computes to 5.5271… × 10^-136, or about 1 in 1,809,251,394,333,065,553,493,296,640,760,748,560,207,343,510,400,633,813,116,524,750,123,642,650,624,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000.
Mathematically speaking, we call this probability not particularly likely.
But just how unlikely is it? A number like that is pretty hard to grasp. Most students take the ACT two or three times. Let’s assume that you’re going to take the test 1,809,251,394,333,065,553,493,296,640,760,748,560,207,343,510,400,633,813,116,524,750,123,642,650,624,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 times, just to make sure you can get the perfect score. We’ll also assume that each attempt takes about 4 and a half hours to work through, including time for a needed snack break. This means your full guess attempts will take about 2.391 × 10^139 seconds, which turns out to be mind-bogglingly large.
How large? Let’s say that your mother is waiting outside the test center while you take your ACT exams. Let’s focus on what she can do while waiting for you to finish. To start, let’s say that she decides to drive around the world. She sets out as you begin your first test and drives until her car runs out of gas. Once it does, instead of buying more, she decides to wait 100 million years for new gas to form deep underground. After that happens, she pumps it back into her car and carries on forwards. She continues on like this, alternating between driving a few hundred miles and waiting 100 million years for more gasoline to form. Slowly but surely, she makes her way around the globe.
Once she reaches your test center again after her 6.2-billion-year journey around the world, she leaves a postcard from her travels. It says “good luck!” written on the back. She then starts her next loop around the world the same way: alternations of driving and waiting for gas formation. Every 6.2 billion-year lap around the planet, she adds another postcard to the stack. Eventually, the stack grows taller and taller until it reaches all the way to the moon. When it does, she removes a single ounce of rock from the moon and takes the stack back down. She then restarts, looping the planet (after waiting for gas to form naturally) and every lap she adds a postcard to the ground. Once the stack reaches the moon again, she takes another ounce from the moon and takes down the stack and starts it all over again.
She continues like this, traveling around the Earth and adding postcards and removing ounces of moon rocks until the entire moon is gone from the night sky. Once the moon is gone, she buys a lottery ticket and stands out in a field. If she fails to win the jackpot, she replaces the moon and starts everything over again. If she wins the jackpot but nothing else exciting happens to her, she also will replace the moon and start all over again. Instead, your mother is waiting for the time when she wins the jackpot and is also struck by lightning, both in the same day. And remember, she’s only buying tickets every time she has completely removed the moon, which she is only removing one ounce at a time after completing a postcard stack all the way up to the moon, which she is building one card at a time, placing one down with each lap driving across the planet with frequent stops for fossil fuel formation.
Anyways, if your mother has won the jackpot and was struck by lightning in the same day, she walks to the nearest beach and removes one grain of sand. Then she starts everything over again! Every time she drives enough loops to stack enough cards to remove enough ounces of the moon to buy a ticket and wins on the same day as being struck by lightning, she removes yet another grain from the Earth until all of Earth’s beaches and deserts are emptied of their sand.
Now, at this point, you might be thinking “surely the testing is close to over at this point.” Well, wrong. If we look at the amount of time remaining, it’s about 2.391 x 10^139 seconds. For reference, we started with a timer of 2.391 × 10^139 seconds. Yes, you read those right. Even after everything so far, we haven’t even see our timer change. All of the time spent so far is lost in the rounding of such an incredibly massive number. Anyways, continuing onwards:
Every time all of Earth’s beaches and deserts are emptied, your mother deals herself a single poker hand. Whenever she gets a royal flush, she squishes a single ant somewhere on Earth, and then—you guessed it—starts everything over again. Once there are no more ants anywhere on the planet, she decides to build a new one: she launches a single pound of dirt into space, and then starts everything all over again. Once she repeats this process enough to have built a second planet Earth floating out in orbit beyond ours, the timer will have finally changed! It has now updated from 2.391 x 10^139 seconds to 2.36 x 10^139 seconds. Finally, some tangible progress!
And so—you know the drill by now—she starts it all back over. She drives around the world with fossil fuel formation breaks. Every lap, she drops a postcard on the floor. Every time the stack reaches the moon, she takes it back down and removes one ounce of moon rocks. When the moon is gone, she buys a lottery ticket. If she won the jackpot and is hit by lightning on the same day, she removes a grain of sand from somewhere on Earth. Every time the beaches and deserts are emptied of all sand, she deals a poker hand, before restoring everything once again. When her poker hand is a royal flush, she squishes a single ant, repeating until all ants are gone, and at that point she begins building yet another Earth out in space one pound of dirt at a time.
Once she has built 78 copies of Earth, and is part-way through building number 79, our timer will finally run out. You’re finally finished with your random-chance ACT perfect score! That wasn’t too hard, now was it? You could have done it with your eyes closed….
As an extra fun fact, remember those snack breaks we mentioned? If you ate a single 2-ounce bag of potato chips for each snack break, by the time you’re done, you’re looking at 1.026× 10^134 kilograms of potato chips. Imagine replacing everything on earth with potato chips. Potato chip Everest, potato chip oceans, and all the like. An entire planet made of potato chips wouldn’t be enough. Imagine that planet has a potato chip moon, and it orbits a potato chip star. Combining the mass of all of those objects, we’re nowhere near close enough. In fact, imagine the Milky Way was really the Potato Way, as every single star and planet and moon and nebula within our galaxy was made of potato. Still not there. Scale up the potatoverse to include all known galaxies and beyond. Dark matter, too. If our entire universe were composed of potato chips, you still don’t have anywhere near enough potato chips for your snack breaks.
It gets worse. If we calculate it out, it turns out that we need 1.026 × 10^81 universes to fit all the matter you’d eat for your snack breaks. For scale, the number of atoms in our non-potato universe is about 1× 10^80. Meaning, if we counted ten potato universes for every atom in our universe, we might have enough for your snack breaks. I hope you’re not counting calories.